Your first program¶
Author: Muhan Li
Full code: Github
This tutorial will guide you to create your first Deep Q Learning (DQN) agent on the CartPole-v0 task. from the OpenAI Gym.
Preface
Some sections of this tutorial are copied and adapted from the Reinforcement Learning (DQN) Tutorial , written by Author: Adam Paszke, credits attributed to him.
Task
The agent has to decide between two actions - moving the cart left or right - so that the pole attached to it stays upright. You can find an official leaderboard with various algorithms and visualizations at the Gym website.
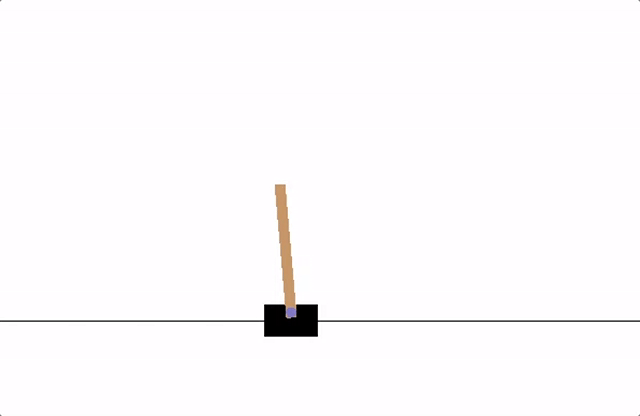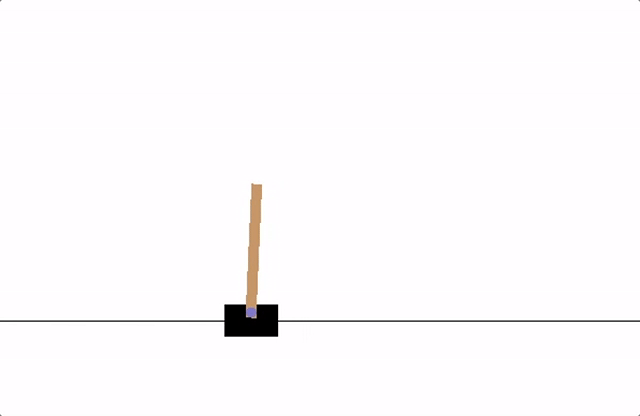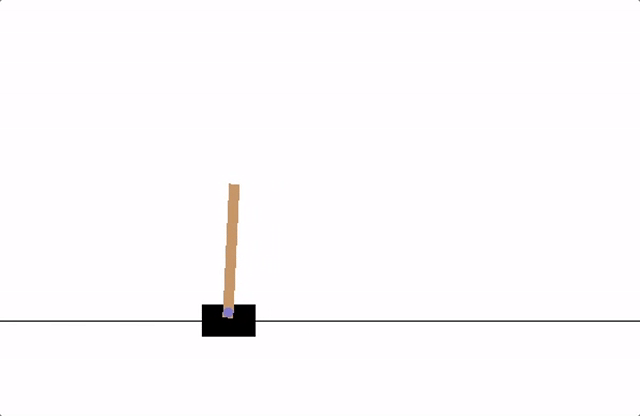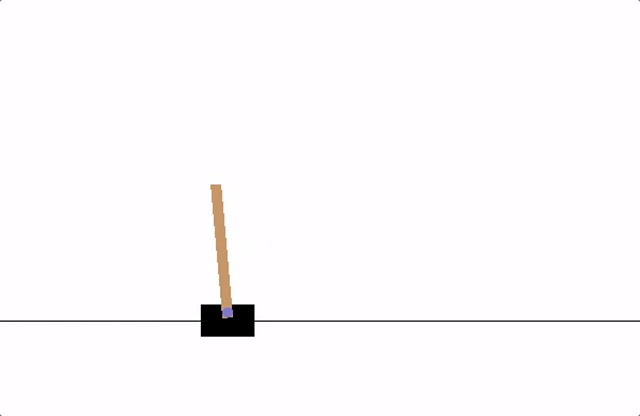
Fig. 1 cartpole¶
As the agent observes the current state of the environment and chooses an action, the environment transitions to a new state, and also returns a reward that indicates the consequences of the action. In this task, rewards are +1 for every incremental timestep and the environment terminates if the pole falls over too far or the cart moves more then 2.4 units away from center. This means better performing scenarios will run for longer duration, accumulating larger return.
The CartPole task is designed so that the inputs to the agent are 4 real values representing the environment state (position, velocity, etc.). However, neural networks can solve the task purely by looking at the scene, so we’ll use a patch of the screen centered on the cart as an input. Because of this, our results aren’t directly comparable to the ones from the official leaderboard - our task is much harder. Unfortunately this does slow down the training, because we have to render all the frames.
Strictly speaking, we will present the state as the difference between the current screen patch and the previous one. This will allow the agent to take the velocity of the pole into account from one image.
A theoretical explanation of DQN¶
Our environment is deterministic, so all equations presented here are also formulated deterministically for the sake of simplicity. In the reinforcement learning literature, they would also contain expectations over stochastic transitions in the environment.
Our aim will be to train a policy that tries to maximize the discounted, cumulative reward \(R_{t_0} = \sum_{t=t_0}^{\infty} \gamma^{t - t_0} r_t\), where \(R_{t_0}\) is also known as the return. The discount, \(\gamma\), should be a constant between \(0\) and \(1\) that ensures the sum converges. It makes rewards from the uncertain far future less important for our agent than the ones in the near future that it can be fairly confident about.
The main idea behind Q-learning is that if we had a function \(Q^*: State \times Action \rightarrow \mathbb{R}\), that could tell us what our return would be, if we were to take an action in a given state, then we could easily construct a policy that maximizes our rewards:
However, we don’t know everything about the world, so we don’t have access to \(Q^*\). But, since neural networks are universal function approximators, we can simply create one and train it to resemble \(Q^*\).
For our training update rule, we’ll use a fact that every \(Q\) function for some policy obeys the Bellman equation:
The difference between the two sides of the equality is known as the temporal difference error, \(\delta\):
To minimise this error, we will use the common MSE loss.
DQN framework¶
The DQN framework is defined in machin.frame.algorithms.dqn, you may import it
with the following statements:
from machin.frame.algorithms import DQN
# Or with the following statement
from machin.frame.algorithms.dqn import DQN
DQN framework is one of the three major types of model-free reinforcement methods supported by Machin. To initialize it, you must at least provide a Q network, a target Q network, an optimizer used to optimize the first Q network, and a criterion used to determine distance between the estimated Q value and the target Q value we would like to reach:
def __init__(self,
qnet: Union[NeuralNetworkModule, nn.Module],
qnet_target: Union[NeuralNetworkModule, nn.Module],
optimizer: Callable,
criterion: Callable,
*_,
lr_scheduler: Callable = None,
lr_scheduler_args: Tuple[Tuple] = None,
lr_scheduler_kwargs: Tuple[Dict] = None,
batch_size: int = 100,
update_rate: float = 0.005,
learning_rate: float = 0.001,
discount: float = 0.99,
gradient_max: float = np.inf,
replay_size: int = 500000,
replay_device: Union[str, t.device] = "cpu",
replay_buffer: Buffer = None,
mode: str = "double",
visualize: bool = False,
visualize_dir: str = "",
**__):...
Your Q network¶
DQN framework supports multiple mode s, the mode parameter could be one of
“vanilla”, “fixed_target” or “double”, for more detailed explanations on these
mode s, please refer to DQN.
Depending on the Q framework mode, your network configurations might be a little
different, by generally speaking, your Q network should accept a state, and then
output estimated Q values for each action. A simple example would be:
class QNet(nn.Module):
def __init__(self, state_dim, action_num):
super(QNet, self).__init__()
self.fc1 = nn.Linear(state_dim, 16)
self.fc2 = nn.Linear(16, 16)
self.fc3 = nn.Linear(16, action_num)
def forward(self, some_state):
a = t.relu(self.fc1(some_state))
a = t.relu(self.fc2(a))
return self.fc3(a)
Please take care of the function signature of forward, because the name of
its arguments will be examined when the DQN framework tries to perform a forward
operation on your Q network, during training or inference.
Now, please remember the name of the state argument: “some_state”.
Optimizer and criterion¶
In order to optimize your model, you must specify an optimizer and a criterion.
Usually the optimizer is torch.optim.Adam. We are going to use the good old
MSE loss nn.MSELoss here.
We have all the ingredients required to start the ignition sequence of the DQN framework, lets mix these parts together:
q_net = QNet(observe_dim, action_num)
q_net_t = QNet(c.observe_dim, c.action_num)
dqn = DQN(q_net, q_net_t,
t.optim.Adam,
nn.MSELoss(reduction='sum'))
The framework might will print two warnings for not setting the input/output device of Q networks, but lets ignore that for now. You may quite Machin down either by:
# to mark the input/output device Manually
# will not work if you move your model to other devices
# after wrapping
q_net = static_module_wrapper(q_net, "cpu", "cpu")
q_net_t = static_module_wrapper(q_net_t, "cpu", "cpu")
Or by:
# to mark the input/output device Automatically
# will not work if you model locates on multiple devices
q_net = dynamic_module_wrapper(q_net)
q_net_t = dynamic_module_wrapper(q_net_t)
static_module_wrapper and dynamic_module_wrapper can be imported from machin.model.nets
Store a step¶
The DQN framework has encapsulated a replay buffer inside, in order to interact with the internal replay buffer, you may use either one of the following APIs, according to your needs:
dqn.store_transition(transition: Union[Transition, Dict])
dqn.store_episode(episode: List[Union[Transition, Dict]])
store_transition stores a single transition step in your MDP process, while
store_episode stores all transitions inside a MDP process.
When you are using other frameworks, these two APIs may both be supported, or only one of them is supported, depending on the internal implementations of frameworks, and requirements of algorithms.
Now lets take DQN as an example, each Transition object describes a single step of
a MDP process, and constitutes of 5 attributes:
state: State observed by your agent when transition begins.
action: Action taken by your agent in this transition step.
next_state: Next state observed by your agent, when action is taken.
reward: Incremental reward given to your agent, due to the taken action.
terminal: Whether the next state is the terminal state of current MDP.
Suppose the observation dimension of your agent is 5, contiguous, within range \((-\infty, +\infty)\), and total number of available discreet actions is 3, then an example transition step would be:
# some states observed by your agent
old_state = state = t.zeros([1, 5])
# suppose action taken by your agent is 2, available actions are 0, 1, 2
action = t.full([1, 1], 2, dtype=t.int)
dqn.store_transition({
"state": {"some_state": old_state},
"action": {"action": action},
"next_state": {"some_state": state},
"reward": 0.1,
"terminal": False
})
Please take note that the sub key of attribute “state” and “next_state” must match the name of the state argument “some_state” in your Q network mentioned above. And the sub key of attribute “action” must be “action”.
We will come back to this seemingly strange name requirement in the Buffer section of Data flow in machin. For now, please make sure that shapes and dictionary keys of your tensors are exactly the same as the example.
Update¶
It is very easy to perform an update step, just call:
dqn.update()
on the framework instance you have just created.
Full training setup¶
With all the necessary parts, we can construct a full training program now:
from machin.frame.algorithms import DQN
from machin.utils.logging import default_logger as logger
import torch as t
import torch.nn as nn
import gym
# configurations
env = gym.make("CartPole-v0")
observe_dim = 4
action_num = 2
max_episodes = 1000
max_steps = 200
solved_reward = 190
solved_repeat = 5
# model definition
class QNet(nn.Module):
def __init__(self, state_dim, action_num):
super(QNet, self).__init__()
self.fc1 = nn.Linear(state_dim, 16)
self.fc2 = nn.Linear(16, 16)
self.fc3 = nn.Linear(16, action_num)
def forward(self, some_state):
a = t.relu(self.fc1(some_state))
a = t.relu(self.fc2(a))
return self.fc3(a)
if __name__ == "__main__":
q_net = QNet(observe_dim, action_num)
q_net_t = QNet(observe_dim, action_num)
dqn = DQN(q_net, q_net_t,
t.optim.Adam,
nn.MSELoss(reduction='sum'))
episode, step, reward_fulfilled = 0, 0, 0
smoothed_total_reward = 0
terminal = False
while episode < max_episodes:
episode += 1
total_reward = 0
terminal = False
step = 0
state = t.tensor(env.reset(), dtype=t.float32).view(1, observe_dim)
while not terminal and step <= max_steps:
step += 1
with t.no_grad():
old_state = state
# agent model inference
action = dqn.act_discrete_with_noise(
{"some_state": old_state}
)
state, reward, terminal, _ = env.step(action.item())
state = t.tensor(state, dtype=t.float32).view(1, observe_dim)
total_reward += reward
dqn.store_transition({
"state": {"some_state": old_state},
"action": {"action": action},
"next_state": {"some_state": state},
"reward": reward,
"terminal": terminal or step == max_steps
})
# update, update more if episode is longer, else less
if episode > 100:
for _ in range(step):
dqn.update()
# show reward
smoothed_total_reward = (smoothed_total_reward * 0.9 +
total_reward * 0.1)
logger.info("Episode {} total reward={:.2f}"
.format(episode, smoothed_total_reward))
if smoothed_total_reward > solved_reward:
reward_fulfilled += 1
if reward_fulfilled >= solved_repeat:
logger.info("Environment solved!")
exit(0)
else:
reward_fulfilled = 0
And your Q network should will be successfully trained within about 300 episodes:
[2020-07-26 22:45:53,764] <INFO>:default_logger:Episode 226 total reward=188.18
[2020-07-26 22:45:54,405] <INFO>:default_logger:Episode 227 total reward=189.36
[2020-07-26 22:45:55,091] <INFO>:default_logger:Episode 228 total reward=190.42
[2020-07-26 22:45:55,729] <INFO>:default_logger:Episode 229 total reward=191.38
[2020-07-26 22:45:56,372] <INFO>:default_logger:Episode 230 total reward=192.24
[2020-07-26 22:45:57,012] <INFO>:default_logger:Episode 231 total reward=193.02
[2020-07-26 22:45:57,658] <INFO>:default_logger:Episode 232 total reward=193.72
[2020-07-26 22:45:57,658] <INFO>:default_logger:Environment solved!